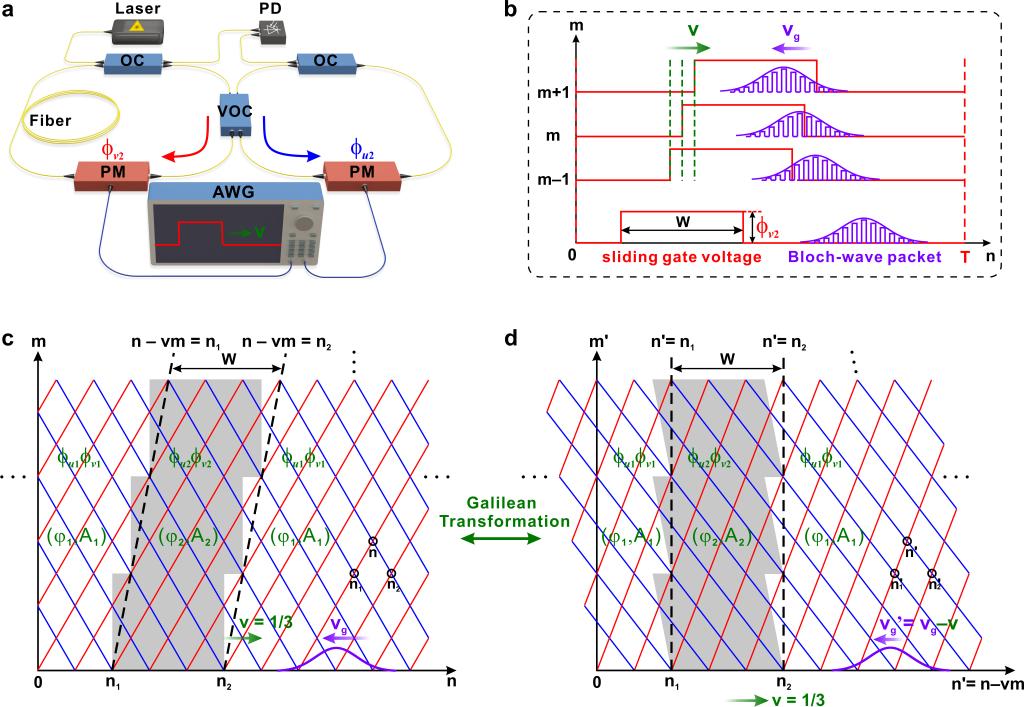
图1.a耦合长-短双光纤环路示意图；b移动门电压信号构造移动矩形势垒示意图；c,d实验室参考系和移动参考系中的离散时域晶格和势垒分布示意图；两种参考系通过伽利略变换相互转换。

6月27日，《自然·通讯》(Nature Communications)在线发表了超快光学实验室在移动光学规范势离散时间折射方面取得的最新研究成果，文章标题为“Observation of discrete-light temporal refraction by moving potentials with broken Galilean invariance”。我院青年教师秦承志副教授为论文第一作者，博士生叶汉(已毕业)和武汉光电国家研究中心博士后王书林为共同第一作者；王兵教授、陆培祥教授和意大利米兰理工大学StefanoLonghi教授为该论文的通讯作者。这项研究得到了国家自然科学基金面上项目、青年科学基金和创新研究群体等项目的资助。

折射是最基本的光学现象，对折射的理解和研究贯穿了整个光学理论和技术的发展历程。传统的折射指的是发生在两种连续介质界面上的光束偏折效应，且遵循斯涅尔折射定律(切向动量守恒)。近年来，随着微纳光学制备技术的快速发展，折射的研究范畴已经从传统连续介质拓展到离散光学结构中如光子晶体、光学波导阵列和光学超材料等；另一方面，随着光学合成维度的研究兴起，折射的概念范畴也已从传统的实空间推广到时间、频率、角动量等光子合成维度和合成空间中，为光场时频调控和信息处理提供了全新的物理机制。

然而，从折射的界面特征来看，目前的研究大都局限于静止界面，而运动界面(如匀速移动的界面或势垒)的折射问题直到最近才有一些理论上的探索。相较于静止界面(或势垒)，移动界面(或势垒)折射的最本质区别是不满足实验室参考系中的斯涅尔定律，原因是移动界面切向方向不是传播方向，不满足界面两侧传播常数守恒；需要采用伽利略变换从实验室参考系得到运动参考系，在运动参考系中界面保持静止从而可以运用斯涅尔折射定律。此外，离散体系的光束传输可以用离散薛定谔方程描述，而离散薛定谔方程不遵循伽利略变换的协变性(即伽利略变换前后形式发生变化)，导致移动界面的离散折射与界面移动速度高度相关。然而，目前关于移动界面的折射对其移动速度的选择定则尚未澄清，而且移动界面或势垒折射的实验论证也尚未见报道。

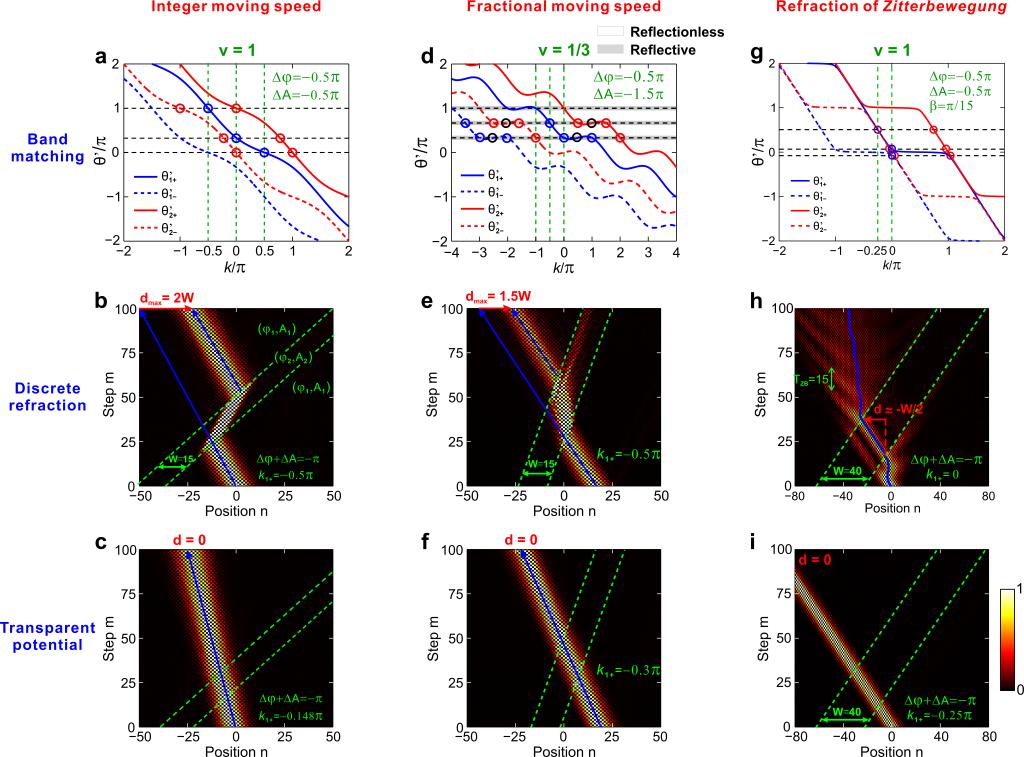
图2.a-c整数移动速度v= 1情形。a移动参考系中势垒内外能带匹配图，蓝(红)线表示势垒外(内)能带，实(虚)线表示+(-)能带支，蓝(红)圈表示入射和折射模式。b,c无反射折射和透明势垒(无折射无反射)情形的光束演化图。d-f分数移动速度v= 1/3的能带匹配图、有反射折射和透明势垒的光束演化图。g-i相对论极限下的狄拉克震颤效应(Zitterbewegung)的折射对应的能带匹配图、离散折射和透明势垒光束演化图。

在这项研究中，研究人员提出在合成时间晶格中构造光子规范势的移动势垒，不仅澄清了移动规范势垒折射对移动速度的选择定则，还揭示了一系列全新离散时间折射规律。团队成员采用耦合双光纤环路构造离散时域晶格(如图1a)，并通过施加移动门电压调制构造移动矩形势垒(如图1b)。研究表明：由于时域晶格的离散本质和双能带特征，移动势垒的折射要消除光束劈裂要求其移动速度满足特定的选择定则(速度的量子化条件)：即移动速度只能取整数v= 1或特定的分数v= 1/q(q为奇数)。在实验中分别选取整数v= 1和分数移动速度v= 1/3，分别实现了无反射和有反射的离散折射(如图2b,2e)，并定量测量了经过势垒两次折射后的唯一光束偏移量，从而验证了无劈裂的折射效应。特别地，通过设计特定势垒高度，光束偏移量还可以为0，从而实现了既无反射又无折射的透明移动势垒(如图2c,2f)。更进一步，通过改变双光纤环路的耦合强度达到弱耦合条件，光束的演化满足狄拉克方程。团队成员还发现了狄拉克震颤效应(Zitterbewegung)的折射，揭示了狄拉克粒子线性能带引起的恒定光束偏移和全布里渊区宽带透明势垒条件。这项研究不仅建立了一系列全新的移动势垒离散折射规律，还发展了移动势垒构造、精密调控以及离散光束折射的表征技术，在光通信、光学信息处理和光场调控方面有着广泛的应用前景。

论文链接为：https://www.nature.com/articles/s41467-024-49747-3